Preventing Premature Entropy Collapse in Maximum Entropy Reinforcement Learning

Deep reinforcement learning has achieved notable results across challenging domains, including robotic manipulation and continuous control tasks. These are problems where agents must output precise, real-valued actions (like joint angles or motor torques) rather than choosing from a fixed set of options. In these settings, an agent's policy, its learned strategy for selecting actions given observations, must balance two competing objectives. Exploration involves trying new actions to discover better strategies, while exploitation means using known effective actions to maximize reward.

Many state-of-the-art algorithms address this tension by encouraging agents to maintain stochastic behavior (randomness in action selection) while maximizing rewards. This approach forms the foundation of maximum entropy reinforcement learning, where policies are trained to succeed at tasks while preserving action diversity ^[1]. The Soft Actor-Critic (SAC) algorithm demonstrates this approach effectively. SAC is an off-policy algorithm, meaning it can learn from experiences collected by previous versions of its policy. This enables strong performance through automatic tuning of a temperature parameter that balances exploration and exploitation ^[2].

Understanding Entropy in Reinforcement Learning

In reinforcement learning, entropy measures the randomness or uncertainty in an agent's action selection. High entropy corresponds to a broader, less concentrated action distribution (more randomness). In other words, the agent is uncertain and exploratory. A policy with low entropy concentrates probability on specific actions, where the agent is confident and exploitative.

Consider a robot learning to navigate a maze. Early in training, the robot knows little about which directions lead to the goal. High-entropy behavior means trying many different paths, gathering information about the environment. As training progresses and the robot discovers successful routes, entropy naturally decreases as the policy commits to effective actions.

Maximum entropy reinforcement learning formalizes this intuition by adding an entropy bonus to the reward objective.

Here, α (the temperature parameter) controls the relative importance of entropy H versus reward r. When α is high, the agent prioritizes maintaining randomness. When α is low, the agent focuses on maximizing reward. This formulation provides several benefits.

• Robust policies that handle unexpected perturbations or environment changes
• Improved exploration that avoids local optima, which are suboptimal solutions that appear best when only nearby alternatives are considered but are inferior to solutions elsewhere in the search space
• Stable training dynamics that prevent premature convergence, where the algorithm settles on a solution before adequately exploring alternatives

A significant challenge accompanies this approach. When the temperature parameter converges too quickly, policies become deterministic before discovering optimal behaviors. This phenomenon, known as entropy collapse, can trap agents in suboptimal solutions. While entropy collapse has been studied extensively in reinforcement learning for language model fine-tuning ^[3], similar dynamics affect continuous control algorithms like SAC, though the specific mechanisms and remedies may differ between domains.

The Entropy Collapse Problem

Entropy can be understood as an exploration budget that depletes during training. In SAC, the temperature parameter α determines how much the agent values randomness relative to reward. The algorithm automatically adjusts α to meet a target entropy level, typically set to −dim(A), where dim(A) represents the action space dimensionality, or the number of independent action variables the agent controls. For example, a robotic arm with seven joints has dim(A) = 7, while a simpler wheeled robot controlling speed and steering has dim(A) = 2 ^[1].

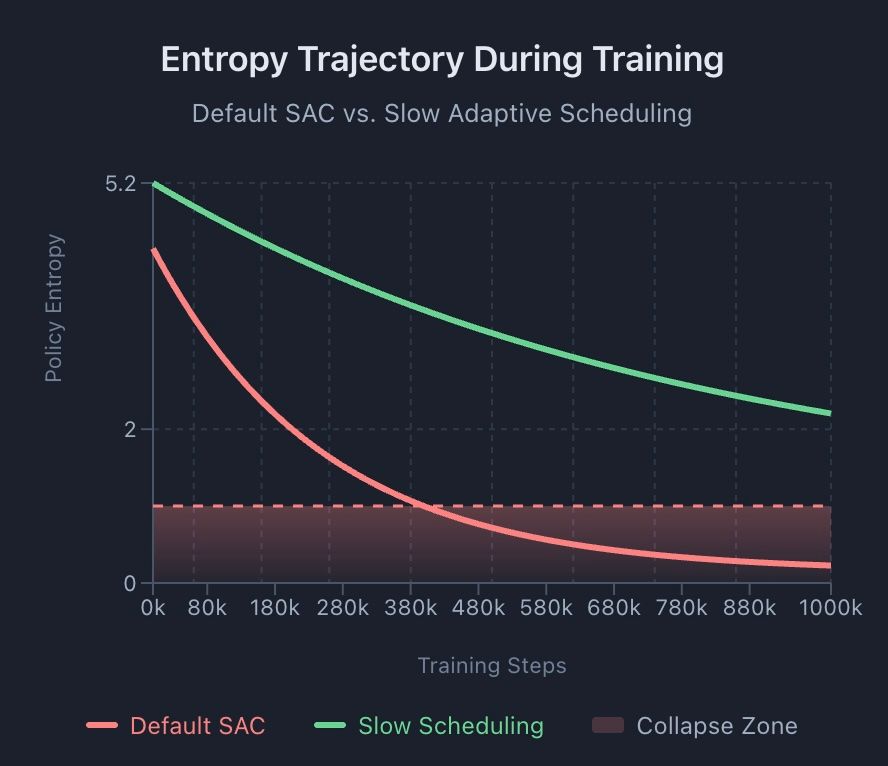
Rapid Entropy Decline (LLM Domain)

Research on RL for language model reasoning (not SAC or continuous control) identifies a pattern where policy entropy drops sharply during early training, reducing exploratory ability and causing performance saturation ^[3]. In that LLM-specific domain, the authors fit an empirical law R = −a·e^H + b relating performance to entropy. This specific quantitative relationship has not been established for SAC or continuous control. However, the qualitative observation that premature entropy decline can limit exploration applies across RL domains.

The problem is particularly pronounced in sparse-reward environments, settings where feedback is infrequent such as a robot that only receives reward upon completing an entire assembly task. It also affects long-horizon tasks that require many sequential decisions before success. Off-policy methods like SAC often struggle in these scenarios due to insufficient exploration, motivating approaches like information-gain maximization to boost exploration ^[4]. When policies become deterministic before discovering critical state-action pairs, agents converge to stable but suboptimal behaviors.

Why Default Tuning Can Fail

SAC's automatic temperature adjustment optimizes α by minimizing the following objective.

The default target entropy H_target = −dim(A) combined with standard learning rates causes rapid α convergence, especially in high-dimensional action spaces. Meta-SAC notes SAC is very sensitive to temperature-related choices (e.g., target entropy and optimization settings), and suboptimal settings can significantly degrade performance ^[2].

The Role of Covariance

Theoretical analysis of RL for language models reveals that entropy dynamics are driven by covariance between policy updates and action probabilities ^[3]. Covariance is a statistical measure of how two variables change together. High-covariance updates occur when the policy's confidence in an action moves in the same direction as its estimated value, causing rapid probability concentration. This theoretical framework was developed for discrete token policies, though similar intuitions about policy update dynamics may apply to continuous control settings.

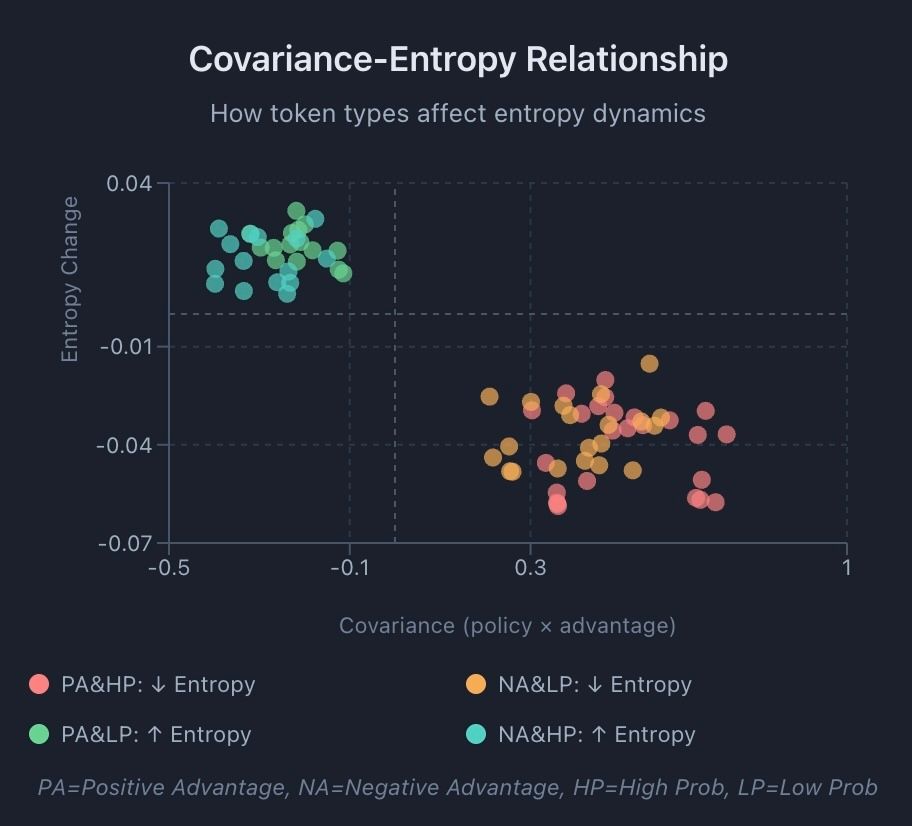
Strategies for Adaptive Entropy Scheduling

Several approaches address premature entropy collapse, each presenting different trade-offs between simplicity and effectiveness.

Reduced Learning Rates for Temperature. A common practitioner heuristic is to reduce the α learning rate relative to policy and critic networks. This slows temperature convergence, maintaining exploration longer. Since SAC is highly sensitive to temperature tuning ^[2], adjusting the learning rate for α can help, though specific reduction factors are not established in the literature and should be determined empirically for each task.

Permissive Target Entropy. The standard SAC heuristic uses H_target = −dim(A), but Meta-SAC notes this is an empirically chosen value that SAC is highly sensitive to ^[2]. Using less aggressive target entropy values (closer to zero) can allow higher policy stochasticity. However, appropriate values are task-specific and depend heavily on action space normalization and squashing functions. In continuous action spaces, SAC uses differential entropy, which can take any real value and is sensitive to scaling, so numeric recommendations do not transfer reliably across implementations.

Entropy Regularization. Adding explicit entropy bonuses to the objective can stabilize training. This technique, called regularization, penalizes undesirable properties such as low entropy. Research on RL for LLM agents identifies a failure mode where conventional entropy regularization becomes counterproductive in multi-turn sparse-reward settings, motivating adaptive phase-based weighting approaches ^[6]. Similarly, work on PPO variants addresses entropy instability through gradient-preserving mechanisms for low-probability actions ^[5].

The Non-Monotonic Entropy-Performance Relationship

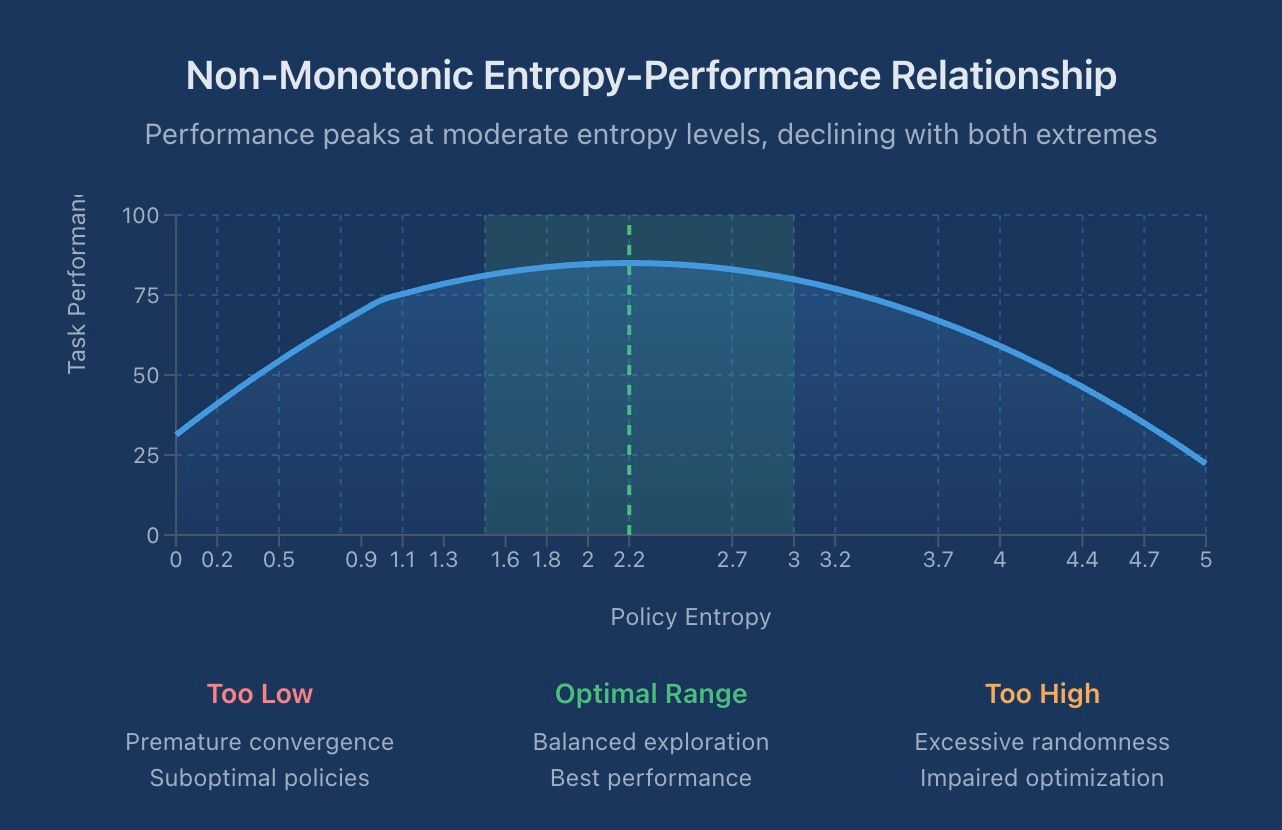
A significant recent finding from reinforcement fine-tuning (RFT) of language models concerns the non-monotonic relationship between entropy and performance ^[7]. This means the relationship doesn't follow a simple "more is better" or "less is better" pattern. Performance initially improves as entropy increases, enabling exploration, but then declines with excessive entropy, which impairs optimization. This reveals an optimal entropy range that varies by task, challenging the assumption that more exploration is always beneficial.

In the RFT domain, this finding suggests that controllable entropy regulation, rather than fixed schedules, may be important for scaling reinforcement learning. Methods that can stabilize entropy at arbitrary target levels while avoiding optimization bias show consistent improvements over entropy-regularized baselines ^[7]. Whether these specific techniques transfer to continuous control remains to be established, though the general principle of task-dependent optimal entropy ranges likely applies broadly.

Connections Across Domains

Much of the recent theoretical work on entropy collapse comes from large language model (LLM) fine-tuning, where reinforcement learning is used to improve model reasoning and alignment ^[3]. In that domain, entropy dynamics impede improvements when models become too confident in particular response patterns too early in training. While LLM policies (discrete token distributions) differ structurally from continuous control policies (Gaussian action distributions), both face the fundamental challenge of balancing exploration and exploitation.

Emerging solutions from the LLM domain include gradient-preserving methods that maintain learning signals from low-probability actions that would otherwise be ignored due to clipping ^[5]. For continuous control, information-gain maximization approaches encourage agents to seek states and actions that provide the most new information about the environment ^[4].

Practical Considerations

For practitioners working with SAC and similar algorithms, the core insight is that default entropy tuning assumptions may be too aggressive for challenging tasks. The standard target entropy heuristic H_target = −dim(A) is empirically chosen and sensitivity to this value is well-documented ^[2]. Monitoring entropy trajectories during training, experimenting with less aggressive targets, and adjusting temperature learning rates represent practical interventions worth exploring. The optimal settings depend heavily on action space characteristics, reward sparsity, and task horizon.

References

[1] Haarnoja, T. et al., "Soft Actor-Critic Algorithms and Applications," arXiv preprint, 2018, Online.

[2] Wang, Y. and Ni, T., "Meta-SAC: Auto-tune the Entropy Temperature of Soft Actor-Critic via Metagradient," arXiv preprint, 2020, Online.

[3] Cui, G. et al., "The Entropy Mechanism of Reinforcement Learning for Reasoning Language Models," arXiv preprint, 2025, Online.

[4] Sukhija, B. et al., "MaxInfoRL: Boosting exploration in reinforcement learning through information gain maximization," arXiv preprint, 2024, Online.

[5] Su, Z. et al., "CE-GPPO: Coordinating Entropy via Gradient-Preserving Clipping Policy Optimization in Reinforcement Learning," arXiv preprint, 2025, Online.

[6] Xu, W. et al., "EPO: Entropy-regularized Policy Optimization for LLM Agents Reinforcement Learning," arXiv preprint, 2025, Online.

[7] Wang, C. et al., "Arbitrary Entropy Policy Optimization: Entropy Is Controllable in Reinforcement Fine-tuning," arXiv preprint, 2025, Online.